러시아 대학, 시험에서 살아남기(СПБГУ 경제학과)

by 유목민 임씨 2023. 10. 1. 08:00

게시물을 올리지 못한 지 거의 한 달이 되었다. 그동안 많은 일이 있었는데 그중 가장 큰 이유는 재시험 때문이었다. 오늘은 러시아 대학 시스템이 어떻게 돌아가며, 대학에 다니고 있는 유학생들이 살아남을 수 있는 팁을 전해주려 한다. 러시아는 가을학기제다. 1학기는 9월 초부터 12월 말까지(12/30 혹은 31일까지) 빡빡하게 진행되며 겨울방학은 굉장히 짧다. 작년 겨울방학 기간에 한국에 일이 있어 잠깐 들어갔었는데 정확히 10일 후에 러시아로 돌아와야 했다. 그만큼 겨울 방학이 짧다. 2학기에는 좀 널널해진다. 여름방학이 길기 때문(7월~8월). 자, 이제 중간고사, 기말고사가 어떻게 진행되는지 알아봐야 한다. 한국에선 대학교에서 F학점을 맞으면 재수강을 해야 한다. 하지만 러시아는 3번의 기회를 주고 100점 중 50점을 넘기지 못하면 퇴학을 시킨다. 필수 전공 시험을 Экзамен, 조금 더 가벼운 과목 시험(예를 들어 철학)을 Зачёт이라고 한다. 이 시험들을 통과하지 못하고 F학점을 받으면 재시험(Пересдача)을 봐야 한다. 여기서도 시험을 못 봐서 F를 받으면 Комиссия라는 살 떨리는 최종 시험을 쳐야 한다.

다른 대학교에서는 공부해 보지 않았으니 СПБГУ를 기준으로 서술하겠다. Зачёт, Экзамен을 러시아 학교에서 공부하지 않고 바로 대학교에 온 학생들은 바로 통과하기가 쉽지 않다. 이유는 이러하다. 아까 50점을 넘겨야 F학점을 받는 것을 면할 수 있다고 했는데 사실 시험에서는 최대 60점을 받을 수 있고 나머지 40점은 출석점수, 과제, 발표점수다. 합산된 점수가 100점이고 이 중 50점을 넘겨야 하는 것이다. 아마 이 게시물은 막 러시아 대학에 진학한 1학년이거나, 러시아 대학이 어떻게 돌아가는지 알고싶어 하는 사람일 것이므로 이게 왜 힘든 일인지 설명하겠다. 보통 어학당에서 짧으면 6개월~길면 10개월의 러시아어 공부를 하고 대학에 진학하게 된다. 물론 한국에서 러시아어과에 다니면서 교환학생으로 왔다가 다시 대학에 진학하는 경우도 있고 러시아 학교 Школа를 마치고 온 경우도 있으니 캐바캐이지만 Школа를 졸업한 경우를 제외하고는 거의 비슷하다고 생각한다. 왜냐, Школа를 졸업한 경우 한국어보다 러시아어를 더 잘할 수도 있는 거니까 말이다.

다시 본론으로 돌아와서, 물론 러시아 교수님들도 1학년에 막 입학한 외국인 학생들이 완벽한 러시아어를 구사할 것이라고 기대하지도 않고 그 기대에 부응할 수 있는 사람도 거의 없다. 발표같은 경우 아무리 완벽하게 준비해도 발표를 무사히 마치는 것 자체가 대단히 어려운 일이다. 친구에게 부탁해서 문법 수정하고 어떻게든 자연스럽게 택스트를 읽는 정도에 그쳐야 한다. 그래도 만점은 받지 못할 것이다. 출석은 당연히 다 했고, 과제와 발표도 무난하게 했다는 가정 하에, 15~20점을 받았다고 하자. 사실 이것도 굉장히 후하게 쳐 준거다. 나머지 점수 30~35점을 시험으로 메꿔야 한다. 몇 점 만점에? 60점 만점에. 사실 여기서 어느 과인지에 따라 갈리게 된다. 러시아에도 '족보'라는 게 존재하는데, 족보를 열심히 외워서 되는 시험이 있고 안 되는 시험이 있기 때문이다. 물론 족보가 있다고 문제은행처럼 같은 문제들만 출제되는 게 아니라 매년 새로운 문제를 섞어서 내기 때문에 족보는 도움이 될 수 있다는 거지 교과서를 읽어보지 않고 문제만 풀어서 가능하지 않다. 물론 귀차니즘이 강한 교수님들은 문제은행식으로 내기도 하는데 교수님의 성향을 잘 파악해야 하고 선배와 친하게 지낼 수 있다면 선배에게서 알아내야 한다. 다행히도 우리 그룹에는 단체 채팅방이 있고 선배가 모든 과목의 기출을 뿌렸기 때문에 나는 여기에서 큰 문제가 없었다.

시험 뭐 잘 보면 되는거지 뭘 계속 우는소리만 하냐!라고 생각할 수도 있겠다 싶어 시험문제를 공개하려 한다.

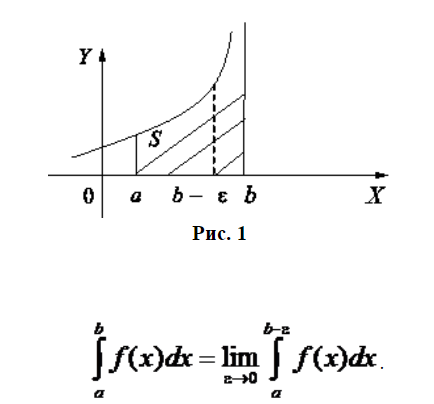
이 시험지는 경제학과 1학년 '수학적 분석'이라는 과목의 시험지이다. 이 수학시험의 경우에는 문제당 두 부분으로 나누어져 있다. "증명"과 "문제풀이"이다. 제일 쉬워 보이는 1번 문제를 살펴보자. 뉴턴-라이프니츠 공식의 특징과 결론을 그래프의 넓이를 이용하여 나타내야 한다. 사실 뉴턴-라이프니츠 공식 f(x)dx = F(b) − F(a) 은 쉬운 공식이라 "뭐 이 정도는.."이라고 생각할 수 있다. 이제 러시아어로 답안지에 서술하면 된다. 여기서 빡치는 건 '러시아어로'이다. 전에 알고 있던 수학 용어들을 러시아어로 싹 다 외워야 한다는 거다.
다음 2번문제. 2형 정적분의 정의를 쓰고, 계산 방법에 대한 근거를 서술하란다. 구글에서 несобственные интеграла 2 рода의 정의를 검색하면 이렇게 나온다

Несобственные интегралы второго рода

Если функция не ограничена на промежутке интегрирования и промежуток интегрирования конечен, то определенный интеграл является несобственным интегралом второго рода.

1. Пусть функция y = f(x) определена и непрерывна на [a,b) и в окрестности точки b функция не ограничена

러시아어만 어렵지 내용은 어렵지 않은데?라고 생각하셨다면 한국말을 끝까지 들어주셔야 한다. 다시 시험지로 돌아와서 오른쪽 위에 86이라는 숫자가 적혀있다. 이건 이 시험에서 출제되는 시험지의 종류가 '적어도 86가지'라는 의미이다. 모든 시험지의 내용이 다 다르고 시험지마다 이런 정의를 러시아어로 적어야 한다. 이렇게 알아야 하는 정의, 증명, 공식들이 얼마나 있었는지 보여드리겠다.

이과로 가면 더하지 덜하진 않을 것이라 확신한다. 상경계인 경제학과, 경영학과에 들어오면 이 '수학적 분석'이라는 과목이 가장 문제이다. 러시아 학생들도 몇몇이 이미 이 과목 때문에 퇴학당했다. 외국인 학생들 특히 중국인 학생들이 이 과목 때문에 50% 이상이 1학기가 끝나자 퇴학당했다. 2학기때는 '재무회계'라는 과목에서 또 몇몇의 중국인과 러시아인 학생들이 퇴학당했다. 나는 어찌어찌 살아남고 있다.

좋은 소식!

Зачёт, Экзамен 에서 나오는 문제와 동일하게 Пересдача가 출제된다. 즉, 시험을 한번 망쳤다고 좌절하지 않고 어떤 문제들이 출제되었는지 열심히 공부하면 2번째 기회인 Пересдача를 통과할 수도 있다. 문제는 괴랄한 범위와 러시아어이다.

좋을 수도 있고 나쁠 수도 있는 소식

1학년때는 교수님들이 외국인 학생의 한계를 알기 때문에 시험 도중에 핸드폰(사전만)을 사용할 수 있게 해 주실 수도 있다. 물론 핸드폰을 쓴다는 것 자체가 부정행위로 연결될 수 있기 때문에 옆에서 감시를 받는다. 심지어 엄격한 교수님이라면 종이사전만 허용할 가능성도 있지만 아예 없는 것보다는 낫다. 하지만 Комиссия에서는 펜, 종이 외에는 모든 게 허용되지 않는다. Комиссия라는 단어 자체가 '위원회'라는 의미가 있는데 학교에서 추방할 학생과 남겨놓을 학생을 결정하는 위원회인 것이다. 해당 과목을 가르치는 모든 교수님(적어도 3명 이상)들이 모여서 학생들의 답변을 같이 채점한다. 이때 채점당하는 학생의 입장이 된다면(이게 나였다) 압박감이 엄청나다. 그럼에도 불구하고 왜 좋을 수도 있는 소식이냐 하면... Комиссия에서는 이미 F를 두 번이나 받은 학생이라는 점을 감안, 40/60으로 나눠서 평가를 하는 게 아니라 그 시험 자체를 100으로 놓고 50점만 넘으면 된다는 것이다. 그리고 이 과목을 특히 못하는 학생들이 오기 때문에 문제를 쉽게 낸다. 쉽게 낸다고 해서 정의, 증명, 공식 등을 몰라도 된다는 건 아니지만 말이다.(수학의 경우) 추가적으로 확신하진 못하지만 다른 시험은 다 통과했는데 딱 한 시험만 통과하지 못했다면 좀 눈감아준다는 이야기가 있다.

수학을 안 한다고 법학과등이 쉽다는 게 아니다.. 러시아 대학에 입학하려고 준비하고 계시는 분이라면 수학을 배우는 과는 좀 더 신중하게 생각해 보시라 말씀드리고 싶다.